1. Verifikation af det fysiske princip i kerneformlen
Lov om bevarelse af masse
Alle formler er baseret på den fysiske natur af m=ρ×V (masse = densitet × volumen)
Densitetsværdi
Teoretisk densitet af rent aluminium: 2.698 kg/m³ (20℃)
Den omtrentlige værdi på 2.700 kg/m³ er rimelig til industrielle beregninger (fejl < 0,1%)
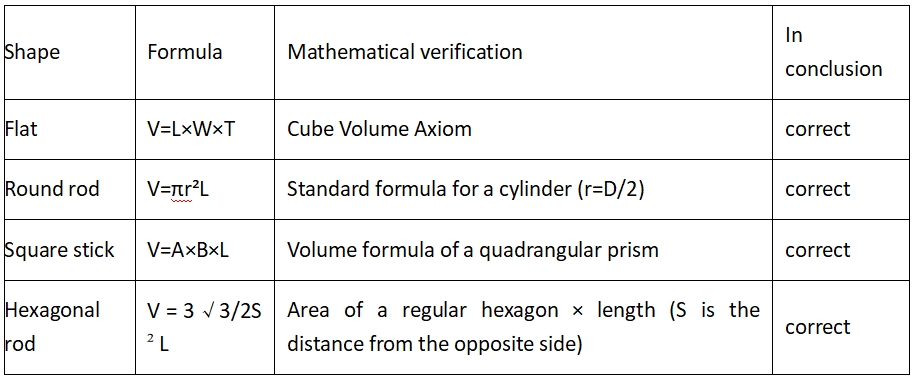
2. Verifikation af geometriske formlers stringens
2.1. Standardformel for geometrisk volumen
Formelbegrænsninger for firkantede rør:
Dette gælder, når rørets vægtykkelse er ensartet, og den indre vinkel er en ret vinkel (det faktiske firkantede rør har en afrundet overgang, og den teoretiske fejl er omkring 1-3%)
3. Verifikation af enhedssystemets konsistens
Undersøgelse af risikopunkter for beregning på tværs af enheder
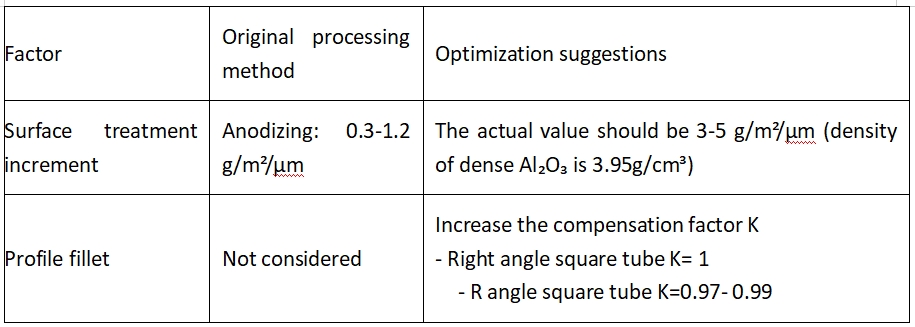
4. Ændring af teknisk egnethed
4.1. Kompensation for ikke-ideelle faktorer
4.2. Kvantificering af tolerancepåvirkning
Tykkelsestolerance ±10% → Vægtafvigelse ±(8% ~ 12%) (tyndvæggede dele er mere følsomme)
Løsning: W faktisk = W teoretisk × (1 + Δt / t) (Δt : tykkelsesafvigelse)
5. Grænsebetingelsestest
Verifikation af ekstreme tilfælde:
Scenarie for tæthedsanomali
7xxx-legering (7075): Målt densitet 2,810 g/cm³ → Hvis der ved en fejl anvendes 2,7 g/cm³, er fejlen +4,1%.
Formeltabel
4t(A + B) - 4t² er en standard ingeniørberegning, der beregnes ved at gange sektionens omkreds med vægtykkelsen og derefter trække de fire hjørner fra.
Eksempel på beregning:
1.6061 aluminiumsplade(1000 × 500 × 10 mm, længde 2 m): B = 1000 × 500 × 2 × 0,0027 = 27 kg
2,7075 rundt rør(ydre diameter 50 mm, vægtykkelse 3 mm, længde 1,5 m): W = [(50-3)×3×3,1416×1,5]×0,00283 ≈ 5,65 kg
3. Firkantet rør(40×40×2 mm, længde 3 m): B = [2×2×(40+40-4)×3]×0,0027×0,98 ≈ 2,42 kg
Anbefalet arbejdsgang
1. Vælg densitet → 2. Mål den faktiske størrelse → 3. Vælg kompensationsfaktor → 4. Beregn med formel
Opslagstidspunkt: 17. juni 2025